Introduction
Bernoulli’s principle can be underst ood it with a simple explanation that when fluid goes from a high-diameter pipe to a low-diameter duct, the speed of the fluid increases many times. Yes, it is true, but is it that simple? Not at all. This principle is quite complex, with many formulas and factors controlling it. There are many applications worldwide utilizing this beautiful principle. One of the common examples explaining Bernoulli’s principle is that the pull you feel towards the train in a railway station when a train passes through the platform, and if you are waiting near the platform side, is due to this principle. The moving train causes the pressure to be low near it. This low pressure pulls near objects towards it. Let us see in detail all about Bernoulli’s principle in this article.
What is Bernoulli’s Principle?
The principle states that in a streamlined fluid flow, the sum of different energies along the line will be the same and constant. The three energies are kinetic energy, potential energy, and the external pressure applied to the fluid. Assume that the pipe has a raise from the ground level at one point, then that part of the pipe adds more potential energy due to the height difference. When the pipe diameter reduces in the streamline, the fluid velocity will increase, and as a result, the kinetic energy will increase.
Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.
Bernoulli’s Principle Formula
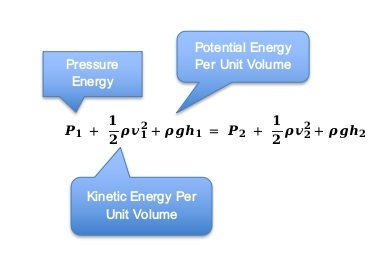
The formula of this concept is more or less connected with the energy conservation law. The total energy of a streamlined fluid flow at any point in time and position in the pipeline is equal. As you refer to the figure below, the c enter portion of the pipe is narrow, and you can observe that the velocity of the fluid and hence the kinetic energy at that portion is more. So, there are such inferences here to discern.

When the diameter of a pipe decrease, the cross-section area reduces, flow speed and pressure increase, and flow rate gets reduced.
P+12ρv2+ρgh=constantP+12ρv2+ρgh=constant
Bernoulli’s Equation Derivation
The two criteria to be remembered while dealing with this equation is that the fluid should not be viscous and the fluid flow should be laminar. Referring to the below diagram, we will derive Bernoulli’s equation.

anonymous, BernoullisLawDerivationDiagram, CC BY-SA 3.0
For the fluid flow to happen, we know there is an external work done, and this work when negotiated with other work like gravitational force results in a pressure difference all along the fluid path. So, work done is given by
W=F1dx1−F2dx2W=F1dx1−F2dx2
dx1=dx1= length of a narrow tube
dx2=dx2= length of a broad tube
Pressure is equivalent to force per unit area.
I.e. P=FAP=FA
So
F=P×AF=P×A
Substituting for force in above equation,
dW=P1A1dx1−P2A2dx2dW=P1A1dx1−P2A2dx2
dW=P1dV−P2dV=(P1−P2)dVdW=P1dV−P2dV=(P1−P2)dV
dV=AdxdV=Adx
The variation in kinetic energy is expressed as below.
dK=12m1v21−12m2v22dK=12m1v12−12m2v22
Note, m is the mass and v is the velocity of a section of fluid.
Since, mass=density×volumemass=density×volume
dK=12ρdV(v22−v21)dK=12ρdV(v22−v12)
Now to find the change in potential energy,
dU=mgh2−mgh1=ρdVg(h2−h1)dW=dK+dUdU=mgh2−mgh1=ρdVg(h2−h1)dW=dK+dU
(P1−P2)dV=12ρdV(v22−v21)(P1−P2)dV=12ρdV(v22−v12)
Cancelling dV on both sides, we get
(P1−P2)=12ρ(v22−v21)+ρg(h2−h1)(P1−P2)=12ρ(v22−v12)+ρg(h2−h1)
On rearranging, above equation, we get Bernoulli’s equation as given below.
P1+12ρv21+ρgh1=P2+12ρv22+ρgh2P1+12ρv12+ρgh1=P2+12ρv22+ρgh2
Principle of Continuity
The product of the cross-sectional area of the pipe and the velocity of the fluid at any point is always a constant. This is the principle of continuity. If A1A1 and A2A2 is the cross-sectional area of both the ends and V1V1 and V2V2 be the velocity of fluid at the respective ends, then we can write,
A1V1=A2V2A1V1=A2V2
Bernoulli’s Principle Use
The fundamentals of this principle are put together in the design elements of airplane aerodynamics, used in expert studies of fluid dynamics and experiments, and the design study of ferry boats where two boats are tied side by side, along with others.
Relation Between Conservation of Energy and Bernoulli’s Equation
The equation states the principle of lowered pressure when the flow velocity increase in laminar fluid flows. So, for non-viscous fluids, the energy conservation is happening in a mutual way between the energy of motion, static energy, and pressure energy.
Bernoulli’s Equation at Constant Depth
It is a unique way to consider the change in the equation when the “constant depth” scenario is conceived. In this scenario, we need to make both the heights h1 and h2 equal. That is h1=h2. Then the equation simplifies.
P1+12ρv21=P1+12ρv22P1+12ρv12=P1+12ρv22
Bernoulli’s Equation for Static Fluids
The equation can be applied to static fluids, where the fluid is not moving. It is static. That means, we can give the value 0 to v1v1 and v2v2 in the equation. Then the equation reduces to
P1+ρgh1=P2+ρgh2P1+ρgh1=P2+ρgh2
Bernoulli’s Principle Example
Whenever there is a deviation of an object either for a good purpose or as a natural reaction, and this happens due to the movement of air or fluids which are non-viscous, then there is Bernoulli’s principle embedded there.
- Airplanes lift due to high-pressure air generated from the propeller under the wings create a low pressure which lift the plane up.
- When a tornado leashes on top of a fixed roof, the roof flies away when the pressure becomes low due to the tornado’s airspeed on top of the roof.
- A cricket ball swings due to the specific way the bowler throws the ball, and due to the reason, that bowler polishes one hemisphere brightly and keeps the other hemisphere of the ball rough.
- A fast train moving creates a pull due to its sheer speed which creates a low-pressure area in its path for some time. Chimney, atomizer, and so forth, you have a lot of everyday experiences of Bernoulli’s principle.
Leave a Reply