Introduction
Most people are very doubtful about the terminology ‘Potential’. In our school time when we first time listened to this term, we learned that potential is somewhat related to the position. However, it means capacity or strength. The term electric potential represents the strength of electricity.
When we start a study for electricity, the first thing we have to face is a charge. The charge is the base of electronics. It is of two types; positive and negative. As we proceed with the charge, we come to know about the electric field, electric potential, potential energy, dipole, etc. Every single charge or a cluster of charges has its field of influence where we can experience the force of attraction and repulsion or develop potential at every position in that region.
What is Electric Potential?
In simple language, we can say that the electric potential for a point in a region where the effective electric field is present, is a piece of work we have to do to change the location of a positive point charge of magnitude one coulomb from infinity position to the point which is considered by us at which the effect of the electric field is present which continues exerting electrostatic force.
Hence, electric potential can also be expressed as work done on a unit charge. Volt is the standard measurement unit of Electric potential. Hence, a one-volt electric potential point is the one joule of work that has to be done for bringing a point positive charge which is located at an infinite far position to a target point. The complete process is also under the impact of forces that comes into play because of the electric field.
V=WqV=Wq
Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.
Electric Potential due to a Point Charge
As we all know that every charge and bunch of multiple charges have their region of influence known as the electric field. In that field, we can feel some electrostatic forces. A point charge also creates an electric potential. In the below section, we are going to examine the potential due to point charge.
Electric Potential at a test charge due to A Point Charge
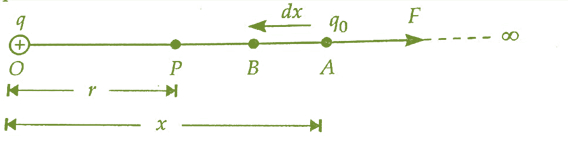
Here, a positive charge q is at point O. Now, we are going to calculate electric potential at a point P which is r distance away from O. As the definition represents that electric potential is equal to the piece of work that is done by us to bring a unit positive charge from the infinite position to the considered point P.
Now, we suppose that there is a test charge q0q0 at x distance far from O point at A.
Using the Coulomb Law, we can find out the force experienced by a test charge because of the q charge,
F=14πϵ0.qq0x2F=14πϵ0.qq0x2
As the force F due to the electric field is working in a direction which is in the opposite direction of the movement of q0q0 charge from location A to location B so we have to do a small amount of work for moving a charge by dxdisplacement against the force exerted by charge.
Hence,
dW=F→.dx−→=F.dxcos180∘dW=F→.dx→=F.dxcos180∘
dW=−FdxdW=−Fdx
The dW is the small amount of work.
The total work needed in the movement of the test charge from any infinite position to point P can find out by integration
W=∫dW=−∫r∞FdxW=∫dW=−∫∞rFdx
W=−∫r∞14πϵ0.qq0x2dxW=−∫∞r14πϵ0.qq0x2dx
W=−qq04πϵ0∫r∞x−2dxW=−qq04πϵ0∫∞rx−2dx
W=−qq04πϵ0[−1x]r∞W=−qq04πϵ0[−1x]∞r
W=qq04πϵ0[1r−1∞]W=qq04πϵ0[1r−1∞]
W=14πϵ0.qq0rW=14πϵ0.qq0r
Thus, from the above expression, the piece of work required to change the position of a test charge from the point which is at an infinite position to the point P is
W=14πϵ0.qq0rW=14πϵ0.qq0r
Now, we know that Potential is
V=Wq0V=Wq0
Hence,
V=14πϵ0.qrV=14πϵ0.qr
Electric Potential due to Multiple Charges
Here we are going to measure the electric potential at any arbitrary point due to a group of N charges. Let there are N point charges i.e q1,q2,q3,q4,q5,q6,q7…..qNq1,q2,q3,q4,q5,q6,q7…..qN are present in the system we considered. All the point charges are r1,r2,r3,r4,r5,r6,r7…..rNr1,r2,r3,r4,r5,r6,r7…..rN distance away from the considered point P.
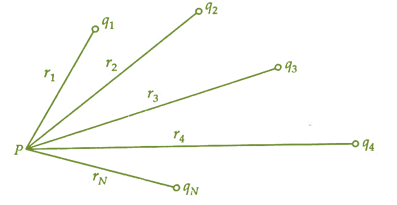
From the last section, we know that the electric potential on any arbitrary point P because of a point charge is
V=14πϵ0.qrV=14πϵ0.qr
For charge q1q1
V1=14πϵ0.q1r1V1=14πϵ0.q1r1
Same like this for other q1,q2,q3,q4,q5,q6,q7…..qNq1,q2,q3,q4,q5,q6,q7…..qN, we get
V1=14πϵ0.q1r1,V2=14πϵ0.q2r2,V3=14πϵ0.q3r3…………VN=14πϵ0.qNrNV1=14πϵ0.q1r1,V2=14πϵ0.q2r2,V3=14πϵ0.q3r3…………VN=14πϵ0.qNrN
We also know that electric potential is not a vector quantity it is a scalar quantity, so for calculating the total electric potential at any point P by N charges will be the sum of the individual potential of every charge.
Thus,
V=V1,V2,V3,V4+……..+VNV=V1,V2,V3,V4+……..+VN
V=14πϵ0.q1r1+14πϵ0.q2r2+14πϵ0.q3r3…………+14πϵ0.qNrNV=14πϵ0.q1r1+14πϵ0.q2r2+14πϵ0.q3r3…………+14πϵ0.qNrN
V=14πϵ0[q1r1+q2r2+q3r3+……+qNrN]V=14πϵ0[q1r1+q2r2+q3r3+……+qNrN]
We can also write the above equation in the form of summation,
V=14πϵ0∑i=1NqiriV=14πϵ0∑i=1Nqiri
This is the total electric potential at any arbitrary point which is here denoted by P in the system of N charges.
Leave a Reply