Introduction
Kirchhoff’s law is used to study the electrical energy used in a circuit. The movement of the charged particles is responsible for electric energy. Energy obtained from the kinetic energy or potential energy of the charged particles is the electric energy. Charged particles are atoms, molecules, or ions that have a charge on them.
There is a force of attraction or repulsion between the charged particles which depends on the coulomb’s law. Electricity flow from one point to another point through a closed path called a circuit. Electric current passes through this closed path. We use many electronic components such as a transistor, resistor, capacitors, etc. Many electronic devices like computers, DVD players etc. are composed of these electronic.
An electrical circuit that is represented graphically is called a circuit diagram. The main application of circuit diagrams is designing, constructing, and maintaining electrical and electronic circuits.
What are Kirchhoff’s Laws?
Gustav Robert Kirchoff was a German physicist who developed circuit laws. He conducted research in many fields of physics such as electric circuits, spectroscopy, and black body radiation.
Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.
Kirchhoff’s First Law
Kirchhoff’s first law is about the current that flows through the circuit. It is also denoted as Kirchhoff’s current law (KCL). According to this law, the total amount of current or the charges that enter the junction or a node is the same as the amount of current or the charges that exit the junction or a node when there is no loss of charge at the node. It can also be stated as the addition of the current that flows in and out of the circuit is equal to zero. It works on the principle of the law of conservation of charges. Thus by the first law of Kirchhoff,
thesumofcurrententeringthecircuit=sumofcurrentleavingthecircuitthesumofcurrententeringthecircuit=sumofcurrentleavingthecircuit
Let us apply Kirchhoff’s first law in the following circuit then we get,
i1+i3+i4=i2+i5i1+i3+i4=i2+i5
By taking the current entering the circuit as positive and leaving the circuit as negative it is also expressed in another form such as
i1−i2+i3+i4−i5=0i1−i2+i3+i4−i5=0
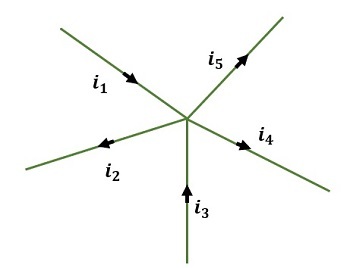
Fig:1 Junction law
Kirchhoff’s law is applies to distributed networks. It does not depend upon the nature of the networks such as active, passive, linear, or nonlinear. Current always flows in the path which has low resistance.
Kirchhoff’s second Law
Kirchhoff’s second law states the voltage drop across the circuit. It is also denoted as Kirchhoff’s voltage law. It is the consequence of both conservations of charges and conservation of energy. The addition of voltage across a closed loop of the circuit in a specific direction is zero. By Ohm’s law voltage across the component is V=IRV=IR
Let us apply Kirchhoff’s second law in the following closed loop we get,
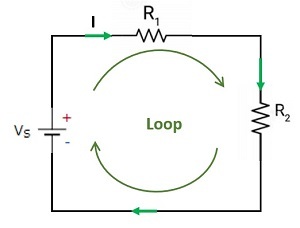
Fig:2 Voltage law
Vs=IR1+IR2Vs=IR1+IR2
KVL is used for all circuits irrespective of the nature of the circuit. It is used in the principle of conservation of charge and energy. In a parallel path, the voltage is constant and in the series path, it is divided.
Generalization of Laws
Initiation of general truth based on observation or experiments that are made between any two phenomena is called generalization of laws. By doing multiple experiments the laws are generalized.
Uses
Kirchhoff’s is used in many areas. If the current passes through the circuit there is a voltage drop across the different circuit areas. Kirchhoff’s law is used to find the amount of current that flows through the circuit and the voltage drop across the circuits. It gives the direction of the current that flows through the circuit.
Advantages
Kirchoff’s law describes the distribution of current in circuits containing many components. It has a way to find the voltage in complicated DC circuits. By this law, one can find the internal resistance of the circuit. One of the best applications of Kirchhoff’s first law is the Wheatstone bridge.
Application
One of the applications of Kirchhoff’s law is Wheatstone’s bridge to find the unknown resistance. it uses both laws. Let us consider four resistance P, Q, R, and S that are connected in a closed loop with the battery and galvanometer in the following manner. Let the current that passes through the resistances P, Q, R, and S are i1,i3,i2i1,i3,i2,and i4i4. The current passing through the galvanometer is ig. Here Kirchhoff’s law is applied to junctions C and F.

Fig:3 Wheatstone bridge
By applying this at the junction C we get,
i1−i3−ig=0i1−i3−ig=0
i1=i3+ig………………………………(1)i1=i3+ig………………………………(1)
At the junction F, we get,
i2+ig−i4=0i2+ig−i4=0
i4=i2+ig………………………………..(2)i4=i2+ig………………………………..(2)
At equilibrium condition ig =0. Then (1) and (2) will become
i1=i3i1=i3
i4=i2i4=i2
Thus Kirchhoff’s first law is applied in a part of Wheatstone’s bridge.
Applying the second law in the loops ACFA and CDFC we get,
i1P+igG−i2R=0……………………………(3)i1P+igG−i2R=0……………………………(3)
i3Q−i4S−igG=0………………………(4)i3Q−i4S−igG=0………………………(4)
At equilibrium condition ig =0. Then (3) and (4) will become
i1P−i2R=0i1P−i2R=0
i1P=i2R………………………..(5)i1P=i2R………………………..(5)
i3Q−i4S=0i3Q−i4S=0
i3Q=i4S……………………………..(6)i3Q=i4S……………………………..(6)
Divide equation (5) by (6)
i1Pi3Q=i2Ri4Si1Pi3Q=i2Ri4S
Here i1=i3i1=i3 and i4=i2i4=i2 So
i1Pi1Q=i2Ri2Si1Pi1Q=i2Ri2S
PQ=RSPQ=RS
By this formula, the unknown resistance in the circuit can be calculated.
Limitations
Kirchhoff’s laws are applicable only for high-frequency AC circuits because of the induced emf due to the magnetic field. Kirchhoff’s current law is applicable for the circuit where the current through the circuit is constant. If there is an assumption that the magnetic field is not changing in a closed circuit, then only the KVL is applicable. It operates on the condition that the electric field in the circuit is neglected.
Leave a Reply