Introduction
Almost all forces in physics are characterized by an associated “field”. The idea, in layman’s terms, is to come up with a quantity that measures the strength of the source of the force.
In physics, field refers to a physical quantity characterized by specific values at different points in space and/or time. It may be represented by a scalar or a vector. In this tutorial, we will discuss a type of field known as the electric field and the units used to measure it.
What is Electric Field?
The electric field is a type of physical field that exists around electrically charged particles and exerts a force on other charged objects around them. The nature of this force depends on the similarity of the two charges in question, the rule being that charges similar in nature repel each other as the like poles of two magnets.
The electric field can be created by an isolated charged particle, a system of many charged particles, or even by a magnetic field that is varying with time. The latter of these cases is a consequence of Faraday’s law.
The value of the electric field at a point may be found by dividing the force experienced by a charged particle by its charge. That is,
E→=F→qE→=F→q
While the above representation suffices in most scenarios, it is often easier to represent problems in electrostatics and electrodynamics in terms of the electric field directly. A better representation of electric field is in terms of the electric potential, in terms of which, we write electric field as −
E→(r→)=−dVdrE→(r→)=−dVdr
Thus, another definition of the electric field is this: “the negative gradient of electric potential gives us the electric field”.
Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.
SI Unit of Electric Field
To derive the SI unit of the electric field, we can use its definition. Since it is the gradient (negative) of the electric potential, its SI units are simply, volt per meter (V/m).
In terms of the base units, the Volt in the numerator may be expanded to give the base representation of the electric field as m⋅kg⋅s−3⋅A−1m⋅kg⋅s−3⋅A−1
Derived Units of Electric Field
One can derive other units for the electric field from its other definitions. Thus, the V/m unit is equivalent to N/C.
Most commonly, we use the SI units of V/m to discuss the Electric field. In terms of value, N/C and V/m are equal and interchangeable.
Significance of Electric Field
Characterizing a System of Charges
Each charge in a system of charges can be treated individually when we are discussing the system itself. However, to understand the effect of this system as a whole on other charges, it doesn’t make sense to work with individual charges.
The electric field is a vector quantity and follows the superposition principle. Thus, using vector addition, we can sum up the values of the electric fields of each of the charges in the system and find a net field. This net field can then be used to describe the effects the system will have on charges around it.
Electrostatic and Electrodynamics Problems
Maxwell’s equations form the fundamentals of electrodynamics, and they treat all problems using electric and magnetic fields. Thus, it makes much more sense to state our problem statements in similar terms as well. This makes further manipulations and calculations easier. Hence, electric fields appear extensively in electrostatic and electrodynamic problems.
Presence of Electric Field Around us
Electric fields are encountered in an enormous number of scenarios. But the most interesting point to note is that without electric fields, this world would not exist! Here is how: we know that atoms are made up of a nucleus surrounded by electrons. These electrons are held in place by the field of the protons in the nucleus. If this electric field were to vanish, the electrons would go flying off out of the atoms and the entire universe would descend into chaos.
Electric Field Lines
If you have ever seen a weather map, you would recall that the flow of wind is represented by arrows and lines. This is not necessary, but it makes understanding wind flow patterns easier. Similarly, an electric field can be represented by drawing lines with arrows in space.
These lines are completely imaginary and only serve as a visual aid to understanding how electric fields are dispersed in a region of space. The direction of the electric field is given by the direction of the arrow, while the length of the line signifies the magnitude. Since electric fields cannot have multiple directions, we can never have two electric field lines that cross each other.
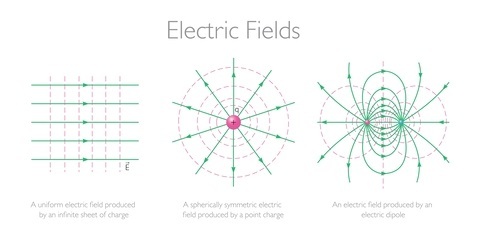
The origin of electric field lines always lies at positive charges. However, the lines may end at negative charges or even at infinity. That is, the direction of electric field lines (and by consequence, the electric field itself) is radially outward from a positive charge and radially inward on a negative charge.
Conclusion
Mathematically, an electric field is simply the amount of force experienced per unit charge. Another definition in terms of electric potential is as follows: the electric field is the negative gradient of electric potential.
From the above definitions, one can find out the SI unit of the electric field, which is Volt per meter, (V/m). This unit is equivalent to Newton per Coulomb, and one can use either of the two units. The origin of electric field lines always lies at positive charges. However, the lines may end at negative charges or even at infinity. That is, the direction of electric field lines is radially outward from a positive charge and radially inward on a negative charge.
Leave a Reply