Introduction
This gaseous theory describes the behavior of the gases contained in some vessels. The particles which are molecules or gases are always in random motion as they continuously move and collide with each other and collide with the container also. Also, there is some pressure and temperature within the container.
The path acquired by molecules is straight and the path is known as the mean free path. after the collision, molecules collide with other molecules instantaneously and thus there is always velocity maintained.
Kinetic Theory of Gases
Gas contains a very huge number of particles whose size is negligible known as molecules. These molecules are in a state of continuous or constant motion or in random motion. During this random motion, molecules continuously move with some velocity and the walls of the container or vessel where it is kept. The collision is so instantaneous.
Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.
Assumption
- Kinetic energy(KE) and momentum(P) will be conserved.
- The size of a gas molecule is negligible(approximately zero).
- No attractive or repulsive force between gas molecules.
- Gas consists of a huge number of tiny particles moving randomly in all possible directions
- center of mass are at rest
- molecules do not exert force on each other or the walls of a container except during a collision.
- The collision between two molecules is perfectly elastic
- molecules of the gases that obey Newton’s laws of motion.
Derivation
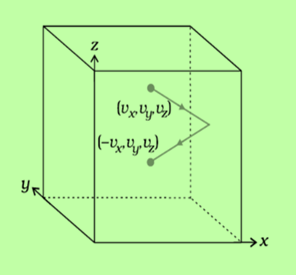
Fig:1 Motion of molecule in a cube
Consider a cubical container containing gas of n number of atoms or molecules peasant in the gas, m mass of each molecule of the gas, and l length of each side of the cube.
Change in the momentum of the molecule,ΔP=P2−P1ΔP=P2−P1
ΔP=mvx−(−mvx)=2mvxΔP=mvx−(−mvx)=2mvx
Time for a consecutive strike,
Time,t=DistanceVelocity=2AvxTime,t=DistanceVelocity=2Avx
Force on the wall,
Force,F=Changeinmomentumchangeintime=ΔPΔt=2mvx2Avx=mv2xlForce,F=Changeinmomentumchangeintime=ΔPΔt=2mvx2Avx=mvx2l
Now,Pressure,P=forcearea=mv2xll2=mv2xl3Pressure,P=forcearea=mvx2ll2=mvx2l3
P=ml2(v2x1+v2x2+v2x3)P=ml2(vx12+vx22+vx32)
P=ml2(Nv2x)P=ml2(Nvx2)
P=mNv2xvP=mNvx2v
Asv2x=v2y=v2zAsvx2=vy2=vz2 or we write v2=3v2xv2=3vx2
v2x=13v2vx2=13v2
PV=13mNv2…….….(1)PV=13mNv2…….….(1)
The Average Kinetic Energy of the Gas Molecule
As we know from the perfect gas equation
PV=nRT……..….(2)PV=nRT……..….(2)
Equating eq (1) and(2), we get
13mV2=nRT13mV2=nRT
Multiplying and dividing by 2
nRT=1223mv2nRT=1223mv2
12mv2=32nRTN12mv2=32nRTN
12mv2=32RTNn12mv2=32RTNn
N – Total no of gas molecules
n – no of moles of gas
12mv2=32RTNA(NA=Nn)12mv2=32RTNA(NA=Nn)
NANA – Avogadro’s number
R – universal constant
T – temperature
m – mass
v – velocity
Avogadro’s number is the no. of molecules present in one mole of gas
Therefore the average KE of gas is given by
K.E=32kT(k=RNA)K.E=32kT(k=RNA)
k – Boltzmann’s constant
For monoatomic molecules, the total internal energy is given by:
ETotal=32PVETotal=32PV
Also, ETotal=32NkTETotal=32NkT
ETotal=32nRTETotal=32nRT
Significance of Kinetic Energy
By knowing the Temperature we can directly figure out the mean Kinetic energy of a gas molecule as the temperature is directly proportional to the kinetic energy of the gas molecules.
The molecules or atoms of any gas are considered but yes gas is taken as an ideal gas.
The kinetic theory of gas is very helpful in understanding the macroscopic parameters like pressure, volume, temperature, or microscopic parameters like kinetic energy, momentum, velocity, etc, and vice-versa of the particles.
Leave a Reply