Introduction
The moment of inertia (MOI) of a body is determined by parallel axis theorem that is parallel to mass of object’s axial line and it also passes through the centre of gravitational force. The PAT suggests that the summation of moment of inertia of a body and product of the mass of a body and square of the axis distances defines the PAT. It helps in finding MOI of objects like rod, discs and a lot more. In this tutorial, the parallel axis theorem will be discussed further.
History of Parallel Axis theorem
The parallel axis theorem was postulated by Christiaan Huygens while he was studying the compound pendulum. The parallel axis theorem is also termed as Huygens-Steiner theorem because it was named after ‘Christian Huygens’ and ‘Jacob Steiner’
Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.
Parallel axis theorem
The parallel axis theorem of an object is used to assess the MOI of a solid and planar body that has an axis line parallel to the axis of the centre of gravity. According to Abdulghany (2017), the moment of inertia of the body determines its condition of existence on a particular plane.
The parallel axis theorem is determined by summation of the inertia of the body around the axis that is moving through midpoint of the mass along with product of the mass of a body multiplied by the square of the distance between two axes (library, 2022). As opined by Wang & Ricardo (2019), this aspect determines the core of the theorem.
This theorem applies to any solid body irrespective of its shape.
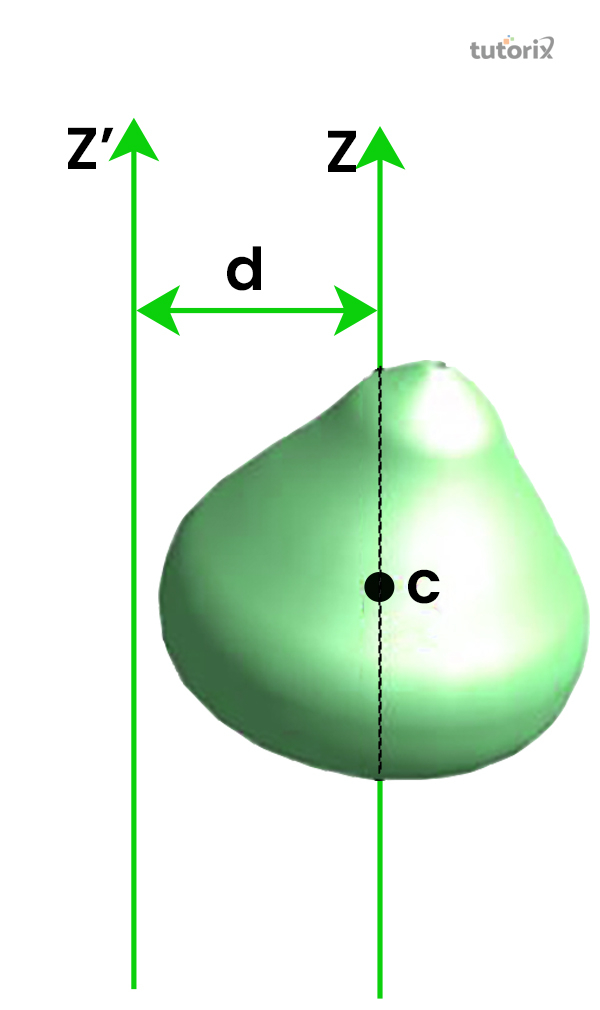
Figure 1: parallel Axes theorem
The formula for the Parallel axis theorem
The parallel axis theorem is associated with the solid bodies and is determined by adding up the moment of inertia of the body with the product of the mass of the body multiplied by the square distance between two axes (phy-astr, 2022).
I = Ix + Ma2
Here,
Here, ‘I’ = moment in the body, Ix = moment of inertia of the particular rigid body and M = mass of the solid object and a2 determines the square of the distance between two particular axes.
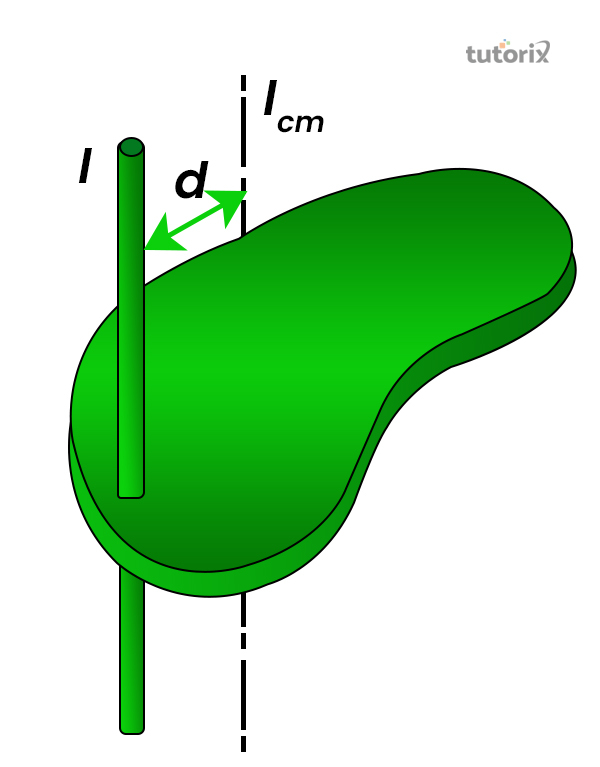
Figure 2: Parallel Axis Theorem
Derivation of the Parallel Axis theorem
This theorem will be able to be derived in the following manner, let, Ix be related with the moment of inertia of a specific solid object and it is moving through the centre of the mass (let the axis be AB) and I will be moment of inertia of body that exists about the axis that is determined using A’B’ and it exists at a distance ‘a’ (phy-astr, 2022).
Now when considering the particle with a mass ‘m’ at a distance ‘r’ from the point that is the centre of the gravity, then it can be derived that A’B’ = r + a
Now
I = Σm ( r + a ) 2
I = ∑m (r2 + a2 + 2ra)
I = ∑m r2 + ∑m a2 + ∑2ra
I = Ix + a2 ∑m + 2a∑m r
I = Ix + Ma2 + 0
I = Ix + Ma2
Parallel Axis theorem of Rod
The parallel axis theorem of the rod will be determined mainly by moment of inertia of the rod. Moment of inertia of the rod is formulated by,
I = ⅓ ML2
Distance between the extreme end of the rod and the centre of the rod is calculated by,
a = L/2
Therefore, the parallel axis theorem is derived in the following manner
Ix = ⅓ ML2 – M(L/2)2
Ix = ⅓ ML2 – 1/4 ML2
Ix = 1/12 ML2
Moment of inertia
It has been previously studied that inertia is associated with the quality of the body exhibits in order to resist a specific state of the linear state of motion be it the object is in motion or is in a state of rest (Rempe et al. 2019). The moment of inertia of an object is indicated through the symbol Im and it is just a measure in which the body is existing in and its associated ability to resist the change in the linear state of motion or a rotational motion.
In both the cases of linear motion and rotational motion, the moment of inertia plays the exact role and thus both the conditions can be compared. Thus it can be established that the moment of inertia associated with a body is its capability to resist the alteration in its state of motion.
That Im = Mr2, here r determines the particles perpendicular distance from its axis of rotation and M is related to mass of the body in a rotational motion. There is however certain factors associated with the moment of inertia, the moment of inertia is a scalar quantity and not a vector quantity, it is not constant for a body as it depends on the rotation of the axis, the moment of inertia of the object is dependent on the mass of the body (phy-astgr, 2022). Greater the mass of the body signifies greater moment of inertia. Subsequently, a greater moment of inertia results in a greater division of the mass from its axis.
Figure 3: Moment of inertia
Application of perpendicular and parallel axis theorem
Perpendicular along with parallel axis theorem is utilized in conjunction for finding moment of inertia of any rigid object about given axis. In order to calculate moment of inertia for any object in rotational motion, parallel along with perpendicular axis theorem are utilized. Parallel axis theorem is utilized when moment of inertia of any object about particular axis is known and is utilized for calculating moment of inertia about axis parallel to any other given axis. Perpendicular axis theorem is utilized for calculating moment of inertia of an object about third perpendicular axis in case of known moment of inertia of object for two perpendicular given axes.
Leave a Reply