Introduction
In a shell model, the basic structure of a particular nucleus is demonstrated. According to this model, the neutrons and protons are situated in separate and different systems of shells. Significant analogous of a shell is also an important part of a shell model. At the outside of a nucleus, electrons are found.
The shell model of the nuclear is an important model, associated with the model of the atomic nucleus. Among various shell models of the nucleus, the first one was introduced by Dmitry Ivanenko in 1932. In a shell model, principles of Pauli exclusion are used.
The basic assumption of a shell model
The base of the structure of a shell model is dependent on the fact that associated with the nucleus. According to a shell model, nucleons that are already situated in a nucleus remain in a definite state. This state is related to angular momentum and energy. Some of the nucleons move in orbit (Shimizu et al 2019). The notion of these nucleons is odd in nature. A strong interaction is also found within this particle system.
Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.
Structure of a nuclei shell model
In order to attain greater stability, the shell model and its structure are important. The arrangement of electrons, available in a nucleus is explained with this model. At the time when a particular shell is filled, the state of the nucleus becomes unusually stable (Hindmarsh & Hijazi, 2019). Each shell possesses a different capability.
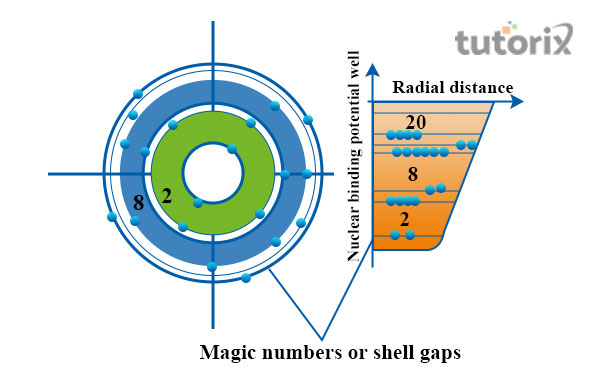
Figure 1: Structure of shell
The atomic number of a nucleus represents the total number of electrons, available in an atom. At a point, protons and neutrons fill the shells of a nucleus. At that time, the total number of n neutrons and protons is regarded as the magic number. The magic numbers are 2, 8, 20, 28, and so on.
The two most important compounds, possessing magic numbers are 208Pb and 40Ca. In these two compounds, a magic number of both protons and neutrons are available and as a result, exceptional stability is found in these nuclei (Stroberg et al. 2019). These compounds are also known as “doubly magic”. There are a total of 6 designation shells in a model and these are K, L, M, N, O, and P. The range of electrons of the P shell is 72 and of O is 50.
Magic number
The total number of nucleons that are present in a singular nucleus is known as the magic number. In the nucleus of a singular atom, the magic number corresponds. The nuclei, possessing a closed shell are found to have a tight bond to the atom. At Z or N, the closing of shells is found to occur (Giesel, Li & Singh, 2021). The nuclei, having an even number of neutrons and protons are more stable in nature than the nuclei with an odd number of neutrons and protons. Doubly magic nuclei are stable and 2He4, 20Ca40, and 8O16 are the three most important among these.
Importance of shell model
The momentum is modified at the time when a paired and a single nucleon get excited. This can happen out of the bottom state and result in modifying the nucleus’s momentum. The reason behind this modification lies in the particles’ parity and projection of isospin quantum numbers (Yoshida & Shimizu, 2021).
A shell is very important as it helps in describing each significant proportion of energy. The energy may be required for maneuvering nucleons from a single orbit to some other orbit. A shell model is helpful in understanding the process of changing quantum numbers.
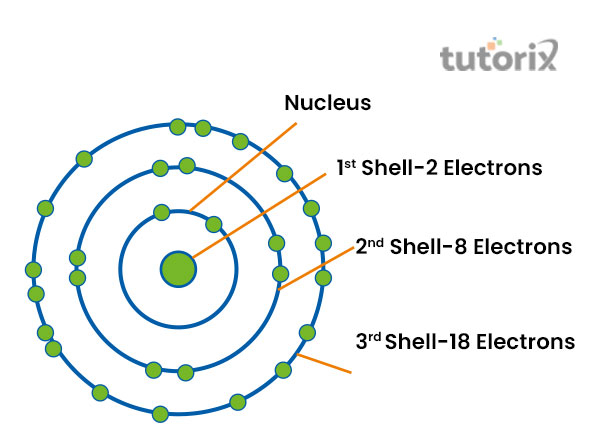
Figure 2: Shell model of Atom
The atomic shell model is important as it helps in explaining the structure of an atom. The atomic numbers are also defined as the total number of electrons, available in an atom. Electrons occupy some of the diffuse shells in a particular space. This is surrounded by
Limitations of a shell model
The difference between wave functions of a shell model and the real state of a nucleus is an important limitation of a shell model. The large value of each significant quadruple moment that is seen in almost all nuclei is very difficult for explaining (Coraggio et al. 2020). The application of interaction regarding strong-spin is mostly difficult by using this method. A very limited application is available for a shell model.
Conclsuion
The energy level is very much different from the principal quantum number. There are some important numbers, associated with the level start of N that is equal to 1. There is no limitation on the angular momentum number that is available in atomic structure. The spin-orbit interaction process helps in splitting the energy level. This split is important as it helps in increasing the value of an orbital quantum number. Overlapping of the energy level is also associated with the energy level of a shell model.
Leave a Reply