Introduction
Initially, electricity and magnetism were treated as separate subjects. In a later period due to the contribution of Oersted, Faraday, Maxwell, etc., it evolved as a unified subject. 
The current-carrying wire creates a magnetic field around it. Faraday through his experiments showed that current can be produced even if there are no batteries in the circuit. The change in the magnetic field can produce a current in the circuit. This result is known as electromagnetic induction. Maxwell tried to write all the main equations of electricity and magnetism in a unified and compact manner. These equations are known as maxwell’s equations.
This set of equations contains – gauss’s theorem of electrostatic, Gauss’ law for magnetism, Ampere’s circuital law, and Faraday’s laws of Electromagnetic induction. Maxwell found some inconsistencies in Ampere’s law. He modified this equation and introduced a new concept called displacement current. Therefore this equation is sometimes also known as the Maxwell-ampere equation.
What is Displacement Current?
James clerk Maxwell introduced this concept. If there is a region where charges are flowing and the electric current is present, then the magnetic field arises due to it. According to Maxwell, in space, the magnetic field arises due to displacement current. Unlike the conventional current, it is not composed of electric charges. Since there is a free space between the plates of the capacitor. We can derive the expression of displacement current by taking the example of a capacitor.
Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.
Displacement Current Equation
To arrive at the displacement current equation, we use the example of a capacitor. We try to find the magnetic field using the ampere’s law –
∮B→.dl→=μ0ienc∮B→.dl→=μ0ienc
Where B = Magnetic field, i = net current passing through the surface.
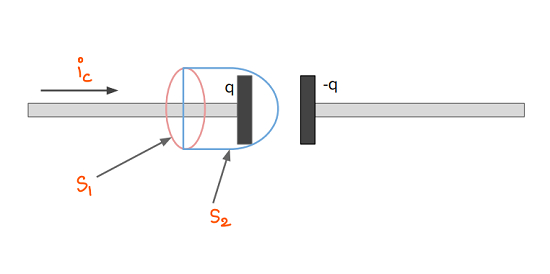
First, we try to calculate the magnetic field by taking surface S1S1. The current passing through this surface is icic. Hence there will be some magnetic field according to ampere’s law. If we take surface S2S2 then there will be no current passing through the surface. This means B→.dl→B→.dl→𝑙zero and non-zero at the same time. It is a contradictory result.
Maxwell solved this problem by introducing a displacement current.
id=ϵ0dϕEdtid=ϵ0dϕEdt
Here idid= Displacement current
ϕEϕE = Electric Flux
We can include this term in ampere’s law.
∮B→.dl→=μ0(ic+id)=μ0ic+μ0ϵ0dϕEdt∮B→.dl→=μ0(ic+id)=μ0ic+μ0ϵ0dϕEdt
It is known as the Maxwell-ampere equation.
If we use this relation, we can resolve the ambiguity arising in the capacitor problem.
For surface S1:i=icS1:i=ic and id=0id=0 since there is no change is electric flux.
For surface S2:i=idS2:i=id and ic=0ic=0 since there are no charges.
Hence, Now the magnetic field will be non-zero for both surfaces.
Characteristics of Displacement Current
The displacement current is produced due to varying electric flux. It can be written as –
id=ϵ0dϕEdtid=ϵ0dϕEdt
It has the following characteristics –
- It is a vector quantity.
- It is measured in Amperes and its dimension are similar to the conventional current.
- It is not produced by the flow of electrons but by the change in the electric field.
- It doesn’t follow ohm’s law.
- For a closed path, it is zero.
- It is not an actual current.
Application of Displacement Current
We can calculate the magnetic field inside a circular capacitor using displacement current.
Suppose the radius of capacitor plates is R, then we imagine a circular wire of radius R between these plates. We take the current flowing in the wire equal to the displacement current idid. We can use the ampere’s circuital law here. Since there is only displacement current between the plates –
∮B→.dl→=B∮dl=B2πr∮B→.dl→=B∮dl=B2πr
r= field point inside the capacitor from the centre.
The electric current is uniformly distributed and the current enclosed by the loop iencienc, is proportional to the area enclosed by the loop. Hence
ienc=idπr2πR2ienc=idπr2πR2
This means
B2πr=μ0iencB2πr=μ0ienc
B2πr=μ0idπr2πR2B2πr=μ0idπr2πR2
B=(μ0id2πR2)rB=(μ0id2πR2)r
It is the magnetic field inside the capacitor. It is inversely proportional to the square of the radius of capacitor plates and directly proportional to the distance between the field point from the center.
We can also calculate the magnetic field outside the circular capacitor, it would be –
B=μ0id2πrB=μ0id2πr
Conclusion
Maxwell found some inconsistencies in the ampere’s law. He modified this equation by introducing a current known as displacement current. Displacement current doesn’t arise from the flow of electric charges but the varying electric flux. Its units and dimension are the same as conventional current.
Leave a Reply