Introduction
In the field of solid mechanics, it can be found that twisting a material by applying a torque on it is denoted as a torsion equation or torsion constant. In various ways, torsion can be expressed. Those possible ways are pascals (Pa), Newton-meters (Nm), or even in foot pound-force (ft. lbf). The SI unit of torsion constant is Newton per square meter (N/m2) or pounds per square inch (p/inc2).
There the process of wrapping is called distortion occurring simultaneously with the occurrence of twisting in non-circular sections. The traverse becomes harsh while the process of wrapping. The equation of torsion is also referred to as the torsion constant. In the case of the derivation of the pure torsion equation, it can be stated that Hooke’s law must be followed along with the content.
It is vital for the circular segment to remain circular. Here the stress of the particles never exceeds its limit of elasticity. The cross-sectional area of the cross-sectional region must remain plane.
What is torsion?

Figure 1: Torsion
In solid mechanics, the torsion is associated with the feature of twisting a particular body because of the application of torque to it. Torsion can further be described in either the scale of Pascal (Pa) or in terms of the SI unit that is Newton per square meter it is also mentioned in terms of pounds per square inch or psi.
However, in contrast to this, the torque is denoted in Newton-meters (Nm) or the foot pound-force. Certain sections in a given object act perpendicular to the acting torque axis. In these particular sites the resultant shear stress is perpendicular to the radius. In a given cross-section that is not circular in shape, a distortion occurs along with the twisting; this particular distortion is termed warping. At the site of warping the transverse section are coarse.
Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.
Torsion constant
The torsion constant is associated with the geometrical property found in the crosssection of a bar, this property exists related to the applied torque through the bar of the axis and the angled formed by the twist. All these particular theories are associated with a homogenous plastic bar. As opined by Atavin et al. (2018), the torsional stiffness of a bar is governed by the torsion constant that is combined with different properties of the object like the length. The SI unit of Torsion constant is denoted by m.
Torsion equation derivation
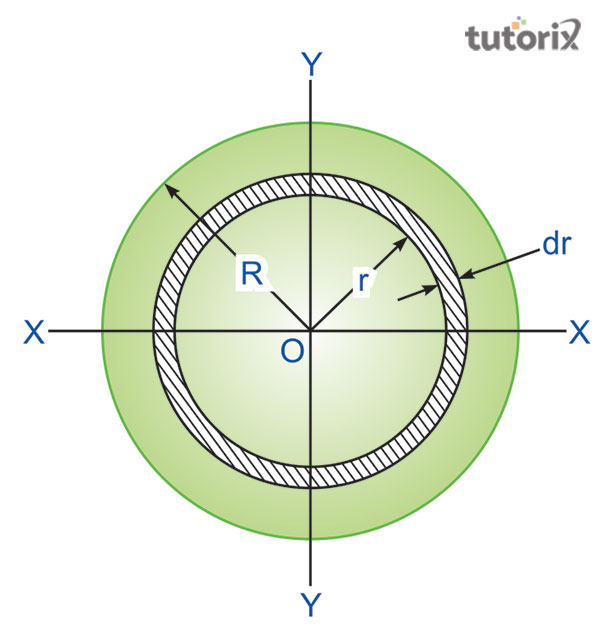
Figure 2: Torsion equation for circular shaft
A solid circular shaft is considered with a designated radius R and it is associated with the torque T that acts on both the ends under the same amount of torque (hkdivedi, 2022).
Angleofradius=arcradiusAngleofradius=arcradius
ArcAB=Rθ=LγArcAB=Rθ=Lγ
γ=RθLγ=RθL
Here, the two distinct fixed points associated with the circular shaft are A and B
And, γ is the angled formed by AB
The modulus of rigidity is denoted by G=τγG=τγ
Here, the shear stress is denoted by𝜏 and the shear strain is denoted by γ
τG=ΓτG=Γ
There it can be established that RθL=τGRθL=τG
A small strip of radius with a thickness dr is considered that undergoes shear stress.
Γ′∗2πrdrΓ′∗2πrdr
Here, r is the radius of a small strip
The thickness of the strip is denoted by dr
The sheer stress is γ
The torque at the centre of the shaft 2πΓ′r2dr2πΓ′r2dr
T=∫R02πΓ′r2drT=∫0R2πΓ′r2dr
T=∫R02πGθLr3drT=∫0R2πGθLr3dr
T=2πGθL∫R0r3dr=GθL[πd432]T=2πGθL∫0Rr3dr=GθL[πd432]
Substituting and integrating the value of R
GθLJGθLJ
Therefore, substitution for polar moment of inertia leads to
TJ=τr=GθLTJ=τr=GθL
Assumption of torsion equation
- The material displays the property of elasticity (Engineeringtoolbox, 2022).
- The object is needed to abide by the Hooke’s law
- The shear stress is out to be proportional to the shear strain
- The area of the cross-section is needed to be plane.
- The circular section is needed to be circular
- The diameter of the material is needed to rotate through a particular angle
- The stress existing in the material should never be higher than the elastic limit
These are assumptions that are needed to be followed by the material to obtain desired results.
Leave a Reply