Tension Force

Introduction

This is the kind of force that is transmissible from various stretchable products like ropes, wires or string. As opined by Kim, et al. (2021), this aspect of tension force is displayed when these products are stretched by the forces that are acting on the opposite ends.

The tension force that is developed is transferred throughout the wire, rope or string. This force pulls an equal amount of energy that is equal on both ends of the objects.

Tension force: definition

Tension in general is associated with the force that has a certain kind of action and reaction forces acting on both of the ends of a particular object. Thus it is established, that the aspect of tension is opposite to that of compression.

According to Mittal et al. (2021), the tension force thus is noted to be acting similarly on both ends of ropes or wires. As opined by Merz et al. (2019), this force exists between these objects when a certain amount of force is transmitted through them as a result of being pulled from opposite ends. The tension force thus derived is redirected throughout a wire and they pull a substantial amount of energy on the ends of the bodies (deutsch 2022).

Therefore it can be established that the tension force is qualified as a pulling source

In the case of classical physics, the ropes are generally considered to be mass less and thus when a mass less rope is presented to a person it can be observed that a force is transferred from one end to another end in a perfect manner. According to Rathnasabapathy et al. (2021), every mass less rope experiences an equal and opposite amount of a tension force. In case the rope is attached to a block and the system is being pulled towards one end the rope evidently experiences tension in one direction and it also experiences tension in another direction due to acquired reactive force from the block.

The tension force acts on flexible objects and it only acts toward a direction that is parallel to the course of that particular flexible medium.

Figure 1: tension force

Tension force: formula

The tension force is denoted by a specific formula that is, T=mg+maT=mg+ma. Here, T is associated with tension, measured by N and m is the mass of the body which is noted in terms of kg (forceinphysics 2022). g is the gravitation force and the value is 9.8m/s29.8m/s2 and a is the acceleration noted by m/s2m/s2.

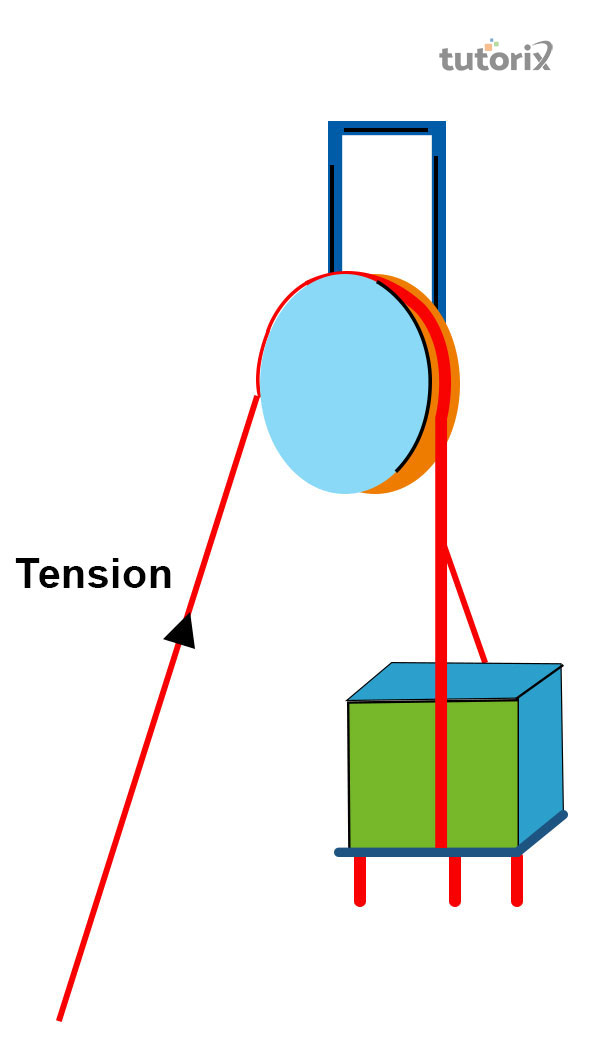
Figure 2: tension

Tension force: examples

Tension force is noted in various bodies and is considered to be a component and is observed in various aspects of daily lives. For example, towing of car when the two truck hook is attached to a car by a steel cable (hk-phy 2022). The resultant force that is formed with the aid of truck is further transferred to the car with the help of cable that helps in pulling the car.

The tension force is noticed in the activity of jumping rope, and a rotational force is produced by the arms of the individuals that help in maintaining the tension in the course of jump. If the force is reduce from the rope the rope slacks down.

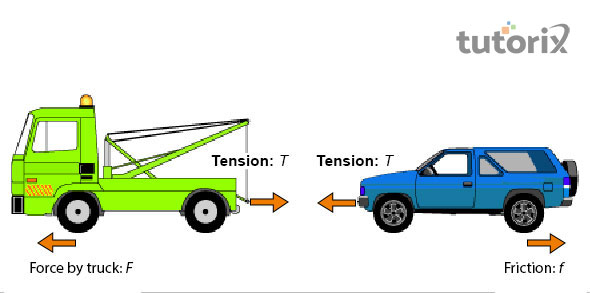
Figure 3: tow truck – tension force

Usage of bow works exhibits the principles of the tension force, a bow usually consists of a flexible body that is made out of wood and a string that is tightly tied to either end of the body that helps in forming the D-shape of the bow, while pulling an arrow the tension that lingered in the body is moved to the string and once let gone, the tension force that was acting on the string helps in the flying motion of the arrow.

While jumping on the trampoline a person can experience the tension force. When a person is trying on jump on the flexible sheet that is tied to the metallic body, the weight of the person pushes down the sheet the tension force on the other hand helps the sheet to retain back to its original shape that makes the person jump higher

Three dimensions of tension

Tension is used to describe a force that is obtained from the ends of three-dimensional continuous materials such as trusses or rods.

As opined by Thomas et al. (2020), this can be noted by the swelling of rods under tension. This stress is thus obtained by the axis force acting per unit of the cross-sectional area.